实验四. 宇宙线缪子飞行时间测量
前言
本实验的目的是:
- 掌握一种测量近光速微观粒子速度的方法。
- 理解系统的固有延迟时间。
一. 实验原理
到达我们实验室的宇宙线缪子打到闪烁体上,大部分能量较高,把两块闪烁体垂直放置,如果方向合适的话,缪子会穿过第一层闪烁体,到达第二层。产生的两个触发信号之间就会有一定的时间差。
我们分别测量分隔一段距离的两层闪烁体的信号时间差,以及紧贴在一起的两层闪烁体的信号时间差。分别做出这两种情况下的信号时间差的直方图。计算他们的差异和飞行距离就可以计算出速度。
二. 实验主要内容
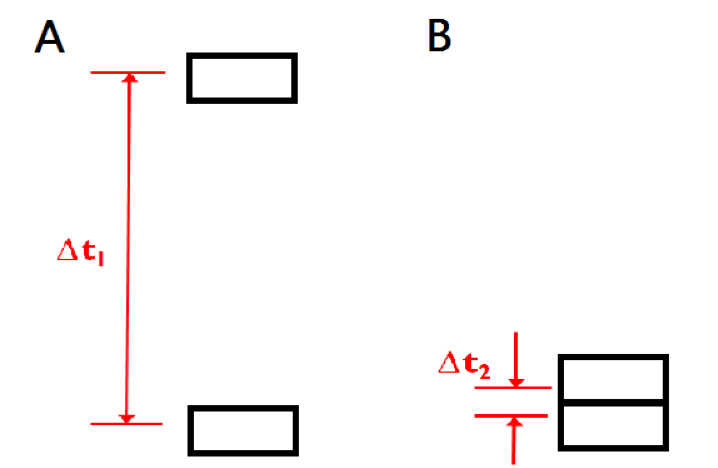
图1:两种情况下搭建实验设备
- 按图1所示的A图搭建设备,两块闪烁体上下分开一米左右,测量A情况时间差分布。
- 按图1所示的B图搭建设备,两块闪烁体紧贴在一起,测量B情况时间差分布,估计两组探测器的固有时间差和时间分辨。
- 测量闪烁体的三维尺寸,及A图中两块闪烁体的间距。
三. 需要观察或测量的问题
- 测量缪子的飞行时间,测量缪子的平均飞行速度。
- 考虑为什么该实验可以用来测量近光速粒子的飞行时间?测量的精度如何?测量设备的关键性质在哪里?
四. 实验步骤
我们先按A情况把两块闪烁体分开放置,图2是A情况实验装置连接图,实验中可以把一块闪烁体放桌上,一块闪烁体放在地上,放在地上的闪烁体位于桌上闪烁体的下方。观察两块闪烁体单端的过阈信号,并且观察这两个信号的符合信号,测量两路信号的时间差。
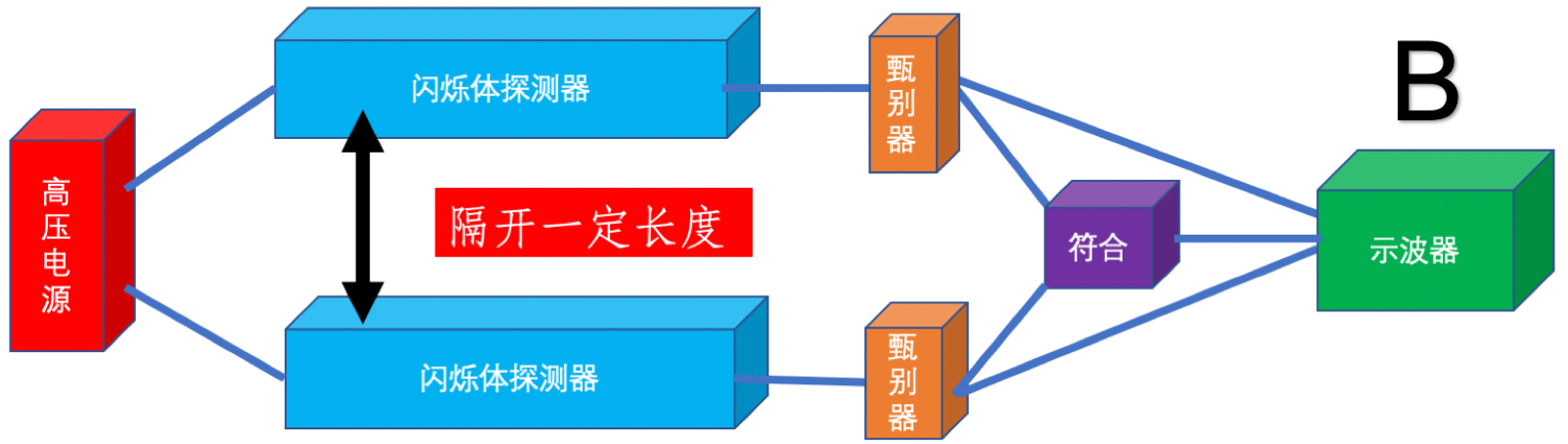
图2:实验装置连接图
然后再按B情况把这两块闪烁体叠放在一起,图3是B情况实验装置连接图。同样观察这种情况下单端的过阈信号和符合信号,测量两路信号的时间差。
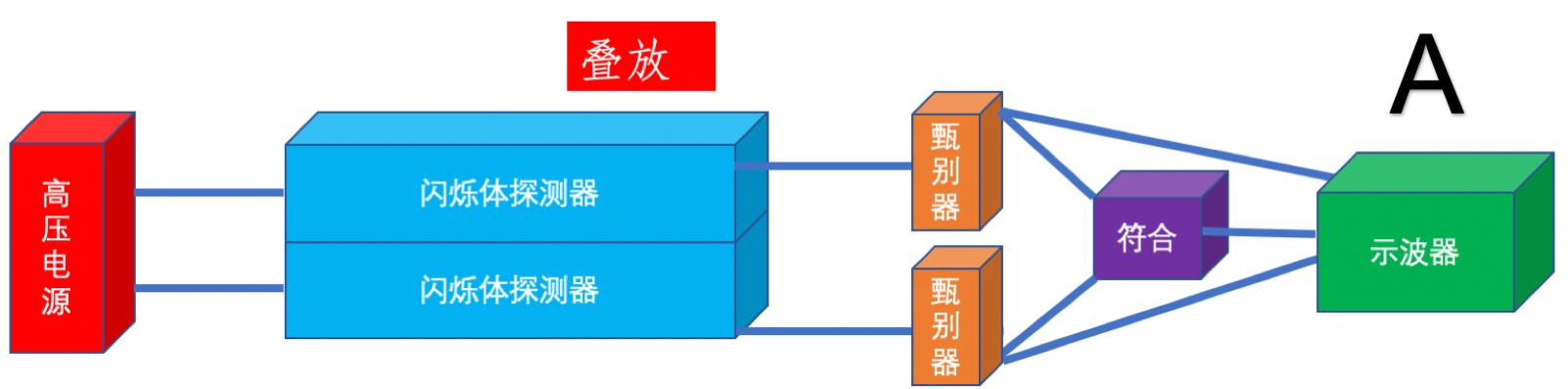
图3:实验装置连接图
观察两种情况下的时间差的直方图,思考其峰值和宽度的含义。
五. 时间差测量
可以利用光标测量两路的时间差,也可以添加时间差的测量项。添加时间差测量项的步骤如图4所示,先按下示波器的measure按钮,添加测量量——延迟。
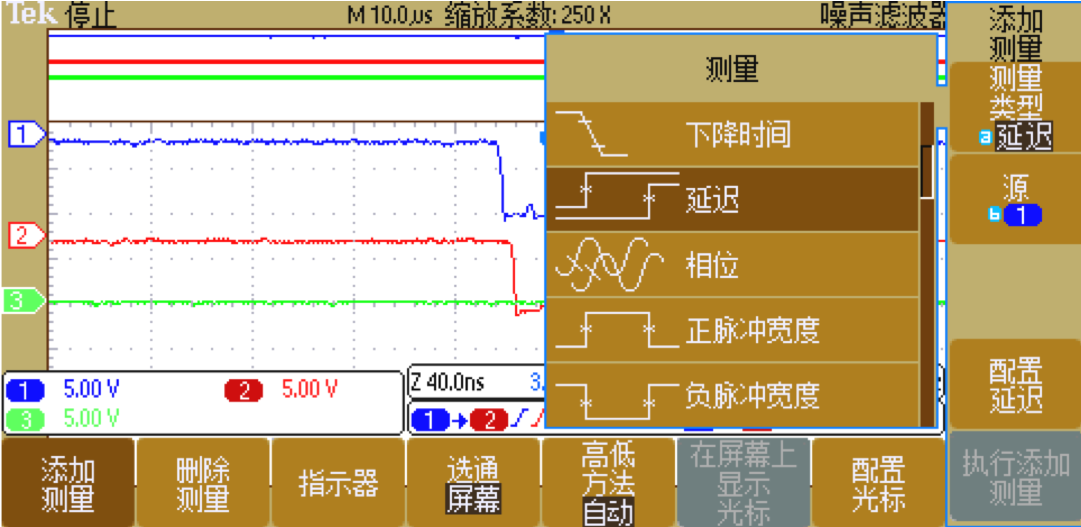
图4:添加测量量——延迟
然后如图5所示配置延迟为两端信号首次下降边沿的时间差,最后按下执行测量量。

图5:配置延迟为两端信号首次下降边沿的时间差
我们可以在示波器上观察到两块闪烁体单端信号和符合信号,如图6所示,并且此时示波器上显示了两个信号下降沿的时间差为5.014ns。
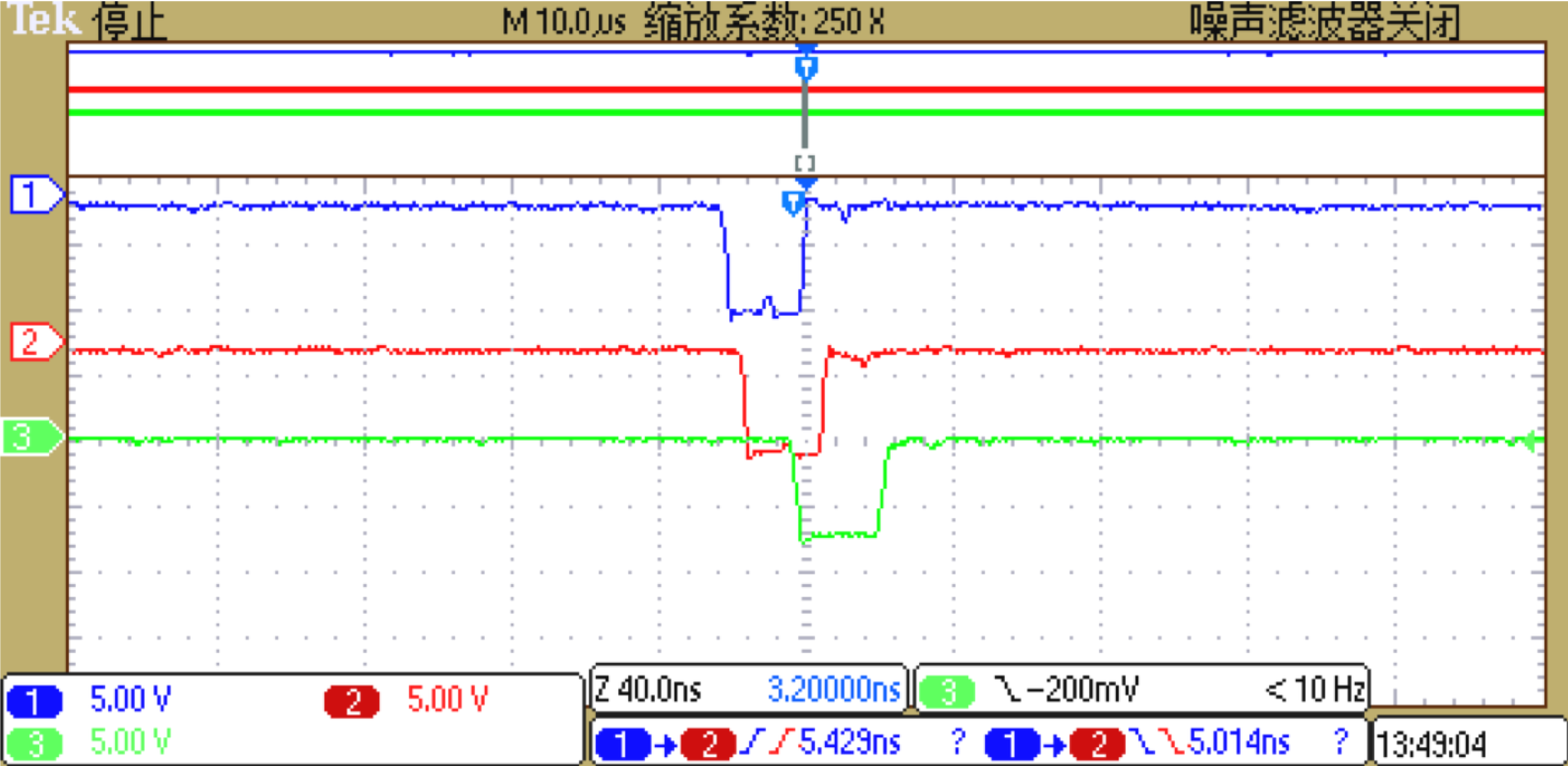
图6:单次缪子飞行的时间差
六. 实验关键点
缪子飞行速度接近光速,穿过1米距离的飞行时间约3 ns,要精确测量这一时间是实验的关键。如下面的公式所示,
每一路的时间测量有很多的延迟和误差,有闪烁体的本征发光时间和光在闪烁体内的传播时间,不确定度在ns量级,PMT自身的时间测量的延迟和延迟,不确定度也在ns量级,还有信号在信号线上的传播时间,示波器的时间测量延迟。而且每一路因采用了不同的PMT和线缆,得到的时间延迟是不一样的,需要一个刻度测量。
- 要有贴在一起的测量,这种情况下粒子的飞行时间近似为0,这种情况下测量得到的时间差为两路之间的固有时间差,可以刻度出两路之间的信号传播的时间差。
- 由上面公式知,有些时延非常大,而且带来的时间晃动也大,可以达到纳秒量级,完全大于待测的时间差3 ns。在高统计量下,利用平均值的误差为 $\sigma/\sqrt{n}$ 的知识,可以显著消除闪烁体发光延时和PMT测量精度的影响。
- 保证两种情况下信号线长度相同来消除信号线长度的影响。
七. 计算缪子飞行速度
可以先考虑最简单的近似情况,可以认为两组不同设置下测量得到的时间分布的峰值的差值为飞行时间,两组闪烁体之间的距离为飞行距离,这样可以得到一个缪子速度测量。
$$v_{\mu}=\frac{h}{\mathrm{d} t}$$
如果需要完整考虑,则要考虑图7的复杂情况。海平面上的缪子存在一个角分布,直射缪子的通量要大于斜射缪子的通量。左边是隔开一定长度的情况,右边是叠放在一起的情况。
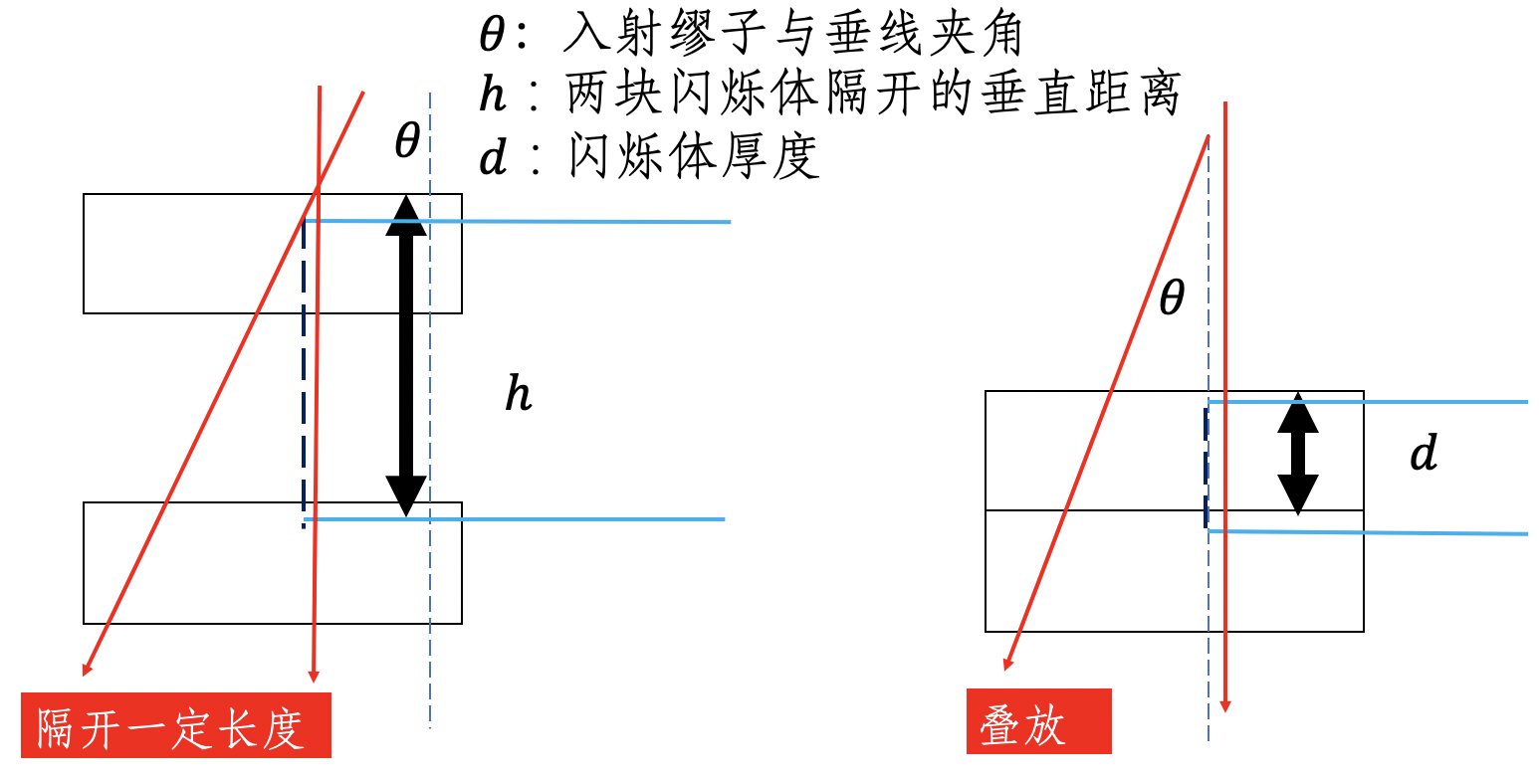
图7:两种情况下缪子可能的路径
在这种复杂情形下,我们需要建模,引入缪子的角分布,系统的模拟两种情况下的时间分布,拟合两种情况下的时间差的数据分布,最终才能导出缪子在空气中的飞行速度。








