Department of Engineering Physics

实验三. 宇宙线缪子寿命测量

前言

本实验的目的是：学习一种测量微观粒子寿命的方法

  1. 从真实的实验测量中理解微观粒子的寿命。
  2. 学习如何在数据拟合中扣除偶然符合本底的贡献。

一. 实验原理

本实验是宇宙线缪子的寿命测量。首先讲一下实验原理，宇宙线粒子与大气中的原子核碰撞大量次级粒子，次级粒子产生缪子。缪子到达我们的闪烁体探测器，会在闪烁体中沉积能量，部分低能的缪子会在闪烁体中沉积完所有能量并停止在闪烁体中，然后发生衰变，

$$\mu^{+} \rightarrow e^{+}+\bar{\nu}_{e}+\nu_{\mu}，$$

$$\mu^{-} \rightarrow e^{-}+\nu_{e}+\bar{\nu}_{\mu}。$$

通过测量初始缪子进入闪烁体的信号和衰变产物的电子在闪烁体内发出的第二个信号之间的时间差，可以测量缪子的寿命。
在粒子物理标准模型理论中，缪子的衰变几率为

$$\lambda_{\mu}=\frac{1}{\tau_{\mu}}=\frac{G_{F}^{2} m_{\mu}^{2} c^{2}}{192 \pi^{3} \hbar^{7}},$$

其中$~\tau_\mu~$是缪子的寿命，也就是平均衰变时间，缪子的静止寿命为$2.2~\mathrm{\mu s}~$ ，静止衰变时放出的电子的动能分布为从$~0 ~\mathrm{MeV}~$至$~53 ~\mathrm{MeV}$（平均值为$~37 ~\mathrm{MeV}$），衰变时间成指数分布。平均衰变时间目前最好的测量结果如下所示：

$$\tau_{\mu}=(2.19703 \pm 0.00004) \times 10^{-6} \mathrm{s},$$

我们采用双端符合的方法来压低热噪声，同时缪子的能量沉积导致的光电子数也要大于热噪声的光电子的单个计数，通过提高触发阈值也可以大量抑制热噪声。 这样，缪子打到闪烁体上能观察到一个符合信号，衰变出来的电子可以观察到一个延迟符合信号，两个信号的时间差预计在微秒量级。 对于实验室中使用的大约$~5 ~\mathrm{cm}~$厚度的闪烁体，有1%的缪子能量较低（动能小于$~10 ~\mathrm{MeV}$），大约为1个/分钟或更低，因此应采用体积更大或更多的闪烁体。 另外，经估计，如果缪子有1 MeV的能量沉积，可以采用较高的阈值，例如100毫伏，进行实验。

二. 实验主要内容

  1. 按照示意图连接好设备，检查信号情况，查看是否有延迟的衰变电子的信号，事例率是否与预估结果相近。
  2. 利用示波器测量缪子触发信号和延迟电子信号之间的时间差，计算平均时间，做寿命测量的粗略估计。
  3. 采集约30分钟数据，利用示波器测量时间，做统计直方图。
  4. 利用最小二乘法拟合实验数据。

三. 需要观察或测量的问题

  1. 如何初始检查信号的质量？
  2. 如何利用最小二乘法去寻找参数的最优值？
  3. 为什么可以用常数项作为偶然符合的本底项？
  4. 如何给出测量结果的误差？
  5. 讨论如何改进我们的实验以克服上面的误差
  6. 考察世界上还有那些实验在测量缪子寿命？
  7. 为什么还要继续测量缪子寿命？

四. 实验步骤

本实验的实验装置连接图如图1所示，

ff

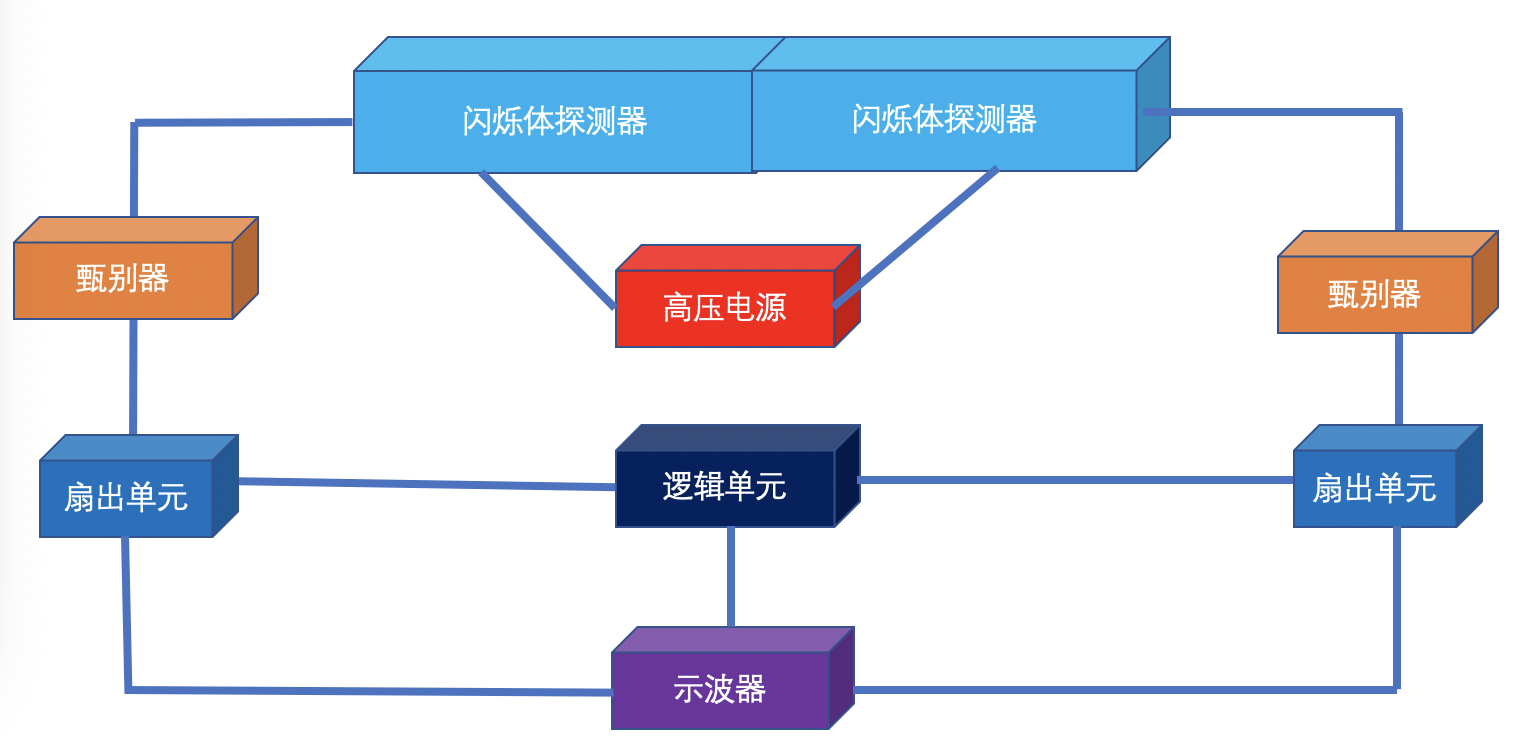
图1：实验装置连接示意图

经过甄别器的双端信号经过扇出单元分别扇出为两路，一路做符合，一路接到示波器上观察。符合后的信号也要接到示波器上。
实验步骤如下，连接好设备后，把每格的时间宽度调节为一微秒，把示波器波形显示的余辉时间调成无穷大。用示波器光标测量缪子触发信号和延迟电子信号之间的时间差。采集30分钟数据，利用示波器的光标测量时间，做统计直方图。用含常数本底项的指数分布来拟合直方图。

$$n_{i}=A \times \exp \left(-t_{i} / \tau\right)+y_{0}$$

其中每个时间bin中观察到的事例数为$m_i$，$t_i$为该bin的平均时间，$A$，$y_0$，$\tau~$为待拟合常数。其中$~A~$为信号部分指数分布前的归一化因子， $y_0~$为一常数本底项，描述偶然符合本底，$\tau~$为待测缪子寿命。

五. 实验注意事项

这个实验有几处需要注意的地方。同学们可以通过适当调节甄别器阈值来压低余波，做实验的时候可以把高压加到1700伏，甄别器设置为100毫伏。本次实验使用光标来测量时间，光标测量的误差为0.02微秒。因为两侧的光标都会贡献误差，所以总的误差为0.03微秒。

$$\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}} \approx 0.03 ~\mathrm{\mu s}$$

连好装置之后，在示波器上可以采样到一个缪子触发的符合信号和微秒量级之后紧跟着的一个符合信号，如图2所示。证明我们观察到了一个缪子衰变的事例。

ff

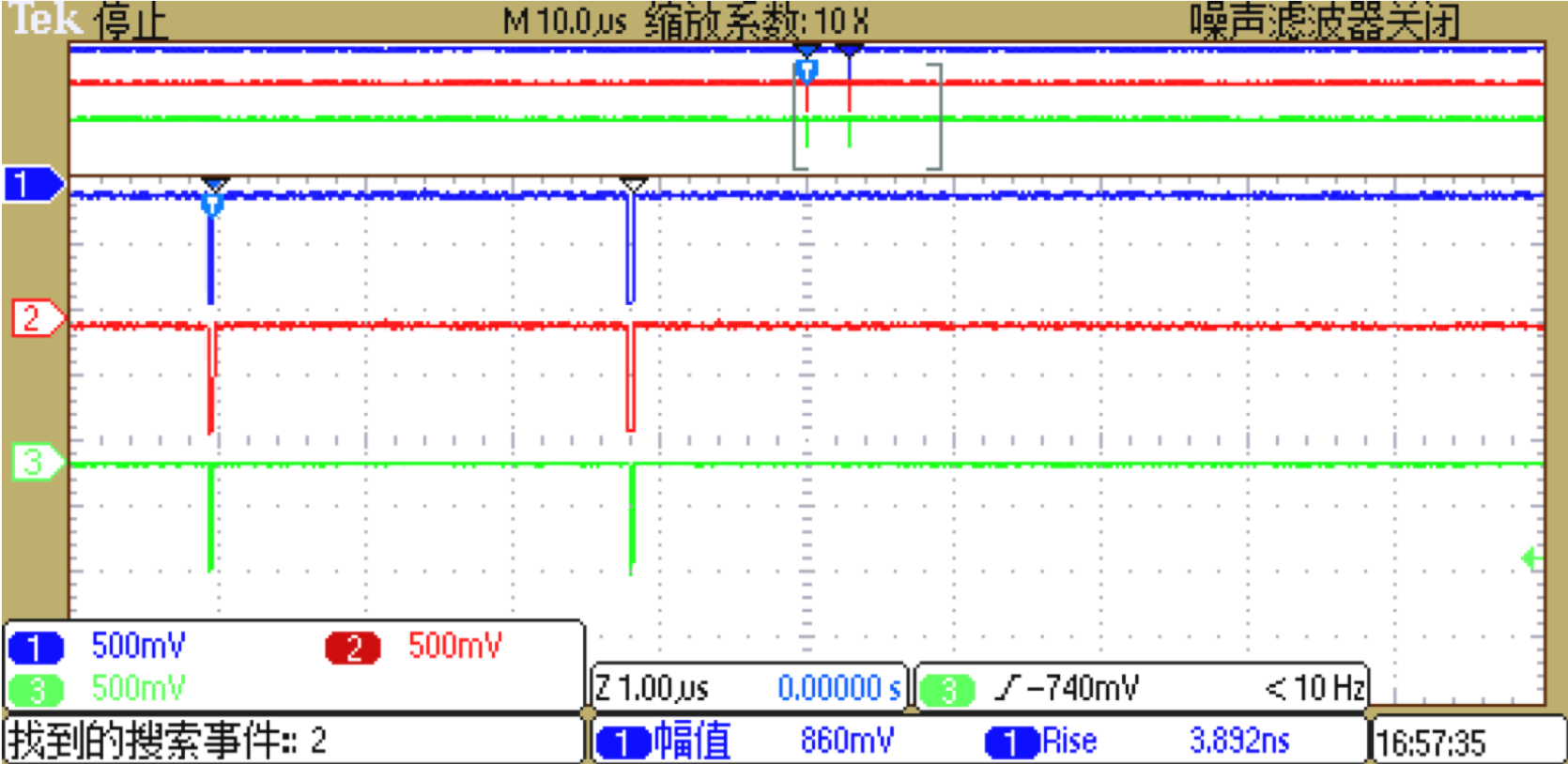
图2：缪子符合信号和缪子衰变信号

下面是用光标测量缪子信号和电子信号时间差的演示视频，通过调节余辉时间为无穷大，显示亮度为100%，我们可以使得缪子衰变的信号停留在示波器上，看到缪子衰变出的电子信号后马上移动光标测量时间差。

六. 实验数据分析

在做实验数据的指数拟合时，有其他的本底存在，例如偶然符合的本底，这些本底的时间结构常数远大于缪子寿命，可以用常数项代替。

拟合时是通过最小化最小二乘法的$~\chi^2~$来得到最优的拟合参数。最小二乘法的$~\chi^2~$可以按如下公式来构造：

$$\chi^{2}=\sum_{i}\left(n_{i}-m_{i}\right)^{2} / n_{i}$$

其中$~m_i~$对应每个时间区间（bin）的统计量。 下图为一典型的时间差分布图及拟合结果（1 TDC=1 ns）：

ff

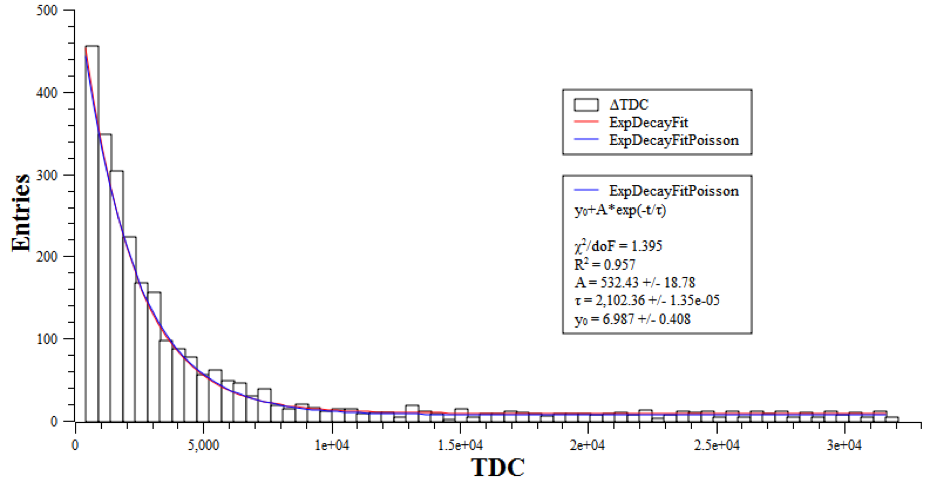
图3：实验数据拟合结果

从图中我们可以看到，拟合结果中包含指数分布的三个参数以及各自的不确定度，还有$~\chi^2~$比上自由度（degrees of freedom），用来衡量拟合结果的好坏。对于固定自由度而言，$~\chi^2~$相比于自由度的差异越小，说明拟合结果越好。

清华大学